yukicoder No.2149 Vanitas Vanitatum

yukicoder.me

はじめに

フック長の公式を初めて触る人が本問題の解説を自分なりに解釈しただけのものになります。表現や厳密性が怪しいところもあるかと思いますが、ご了承下さい。

問題概要

広義単調数列$A_1$、$A_2$、$\cdots$、$A_N$に対して、広義単調が保たれたまま以下の操作を行う。

$A_i \geq 2$となる添え字$i$を選び2を引く。
$A_i = A_{i + 1} \geq 1$となる添え字$i$を選び、それぞれ1を引く。

すべての要素を$A_i = 0$にするのに、何通りの操作があるか。

解法

はじめに、数列の「増加」、「変化なし」を01列に対応させます(増加を1、変化なしを0とする)。入力例として

6
2 2 3 5 6 6

を挙げると、

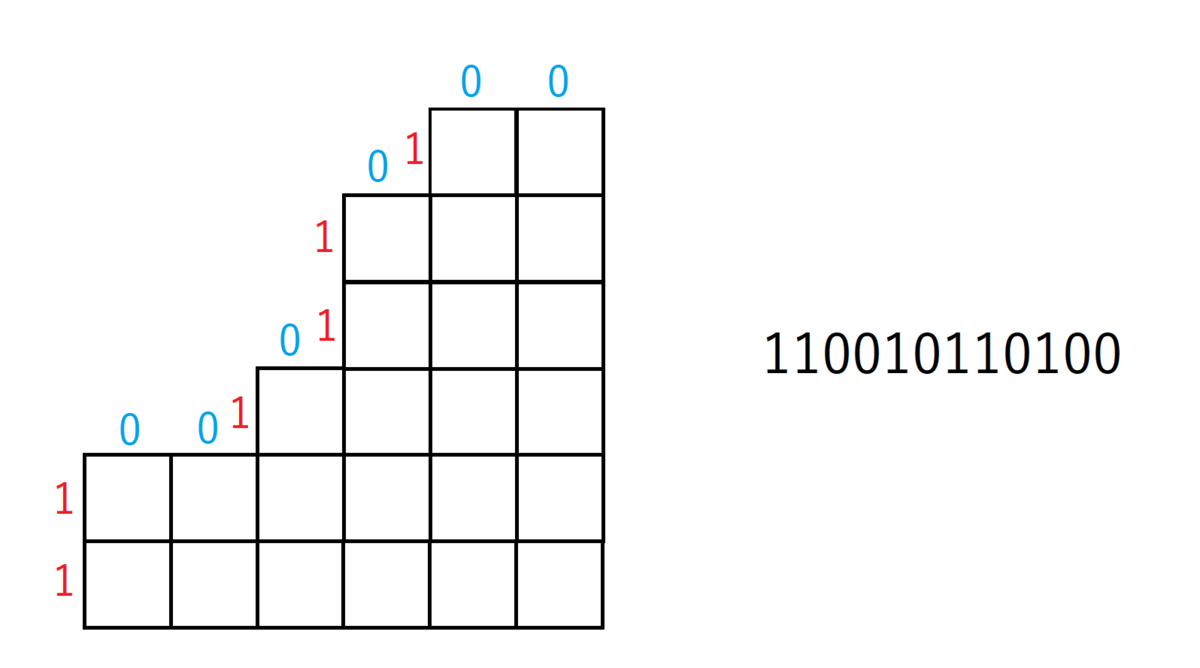
のようになります。それぞれの操作について見ていくと、1つの要素を選んで$-2$を行う操作は、01文字列のうち「110」を「011」に変化させることに相当します。

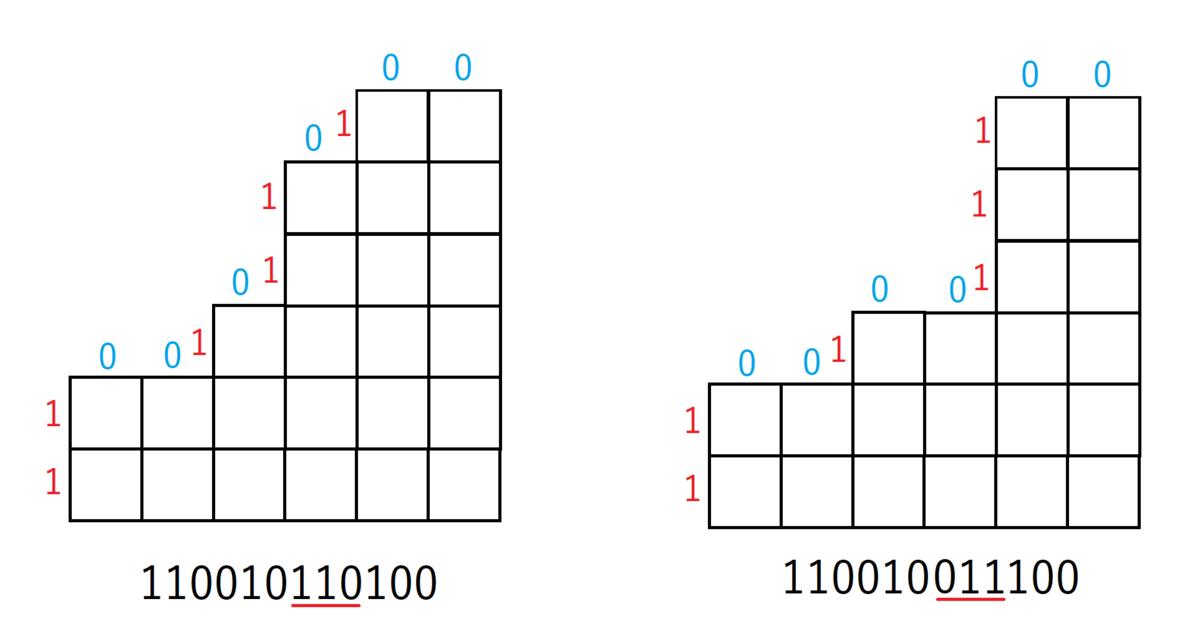
一方、隣接する2つの要素を選んで$-1$を行う操作は「100」を「001」に変化させることに相当します。

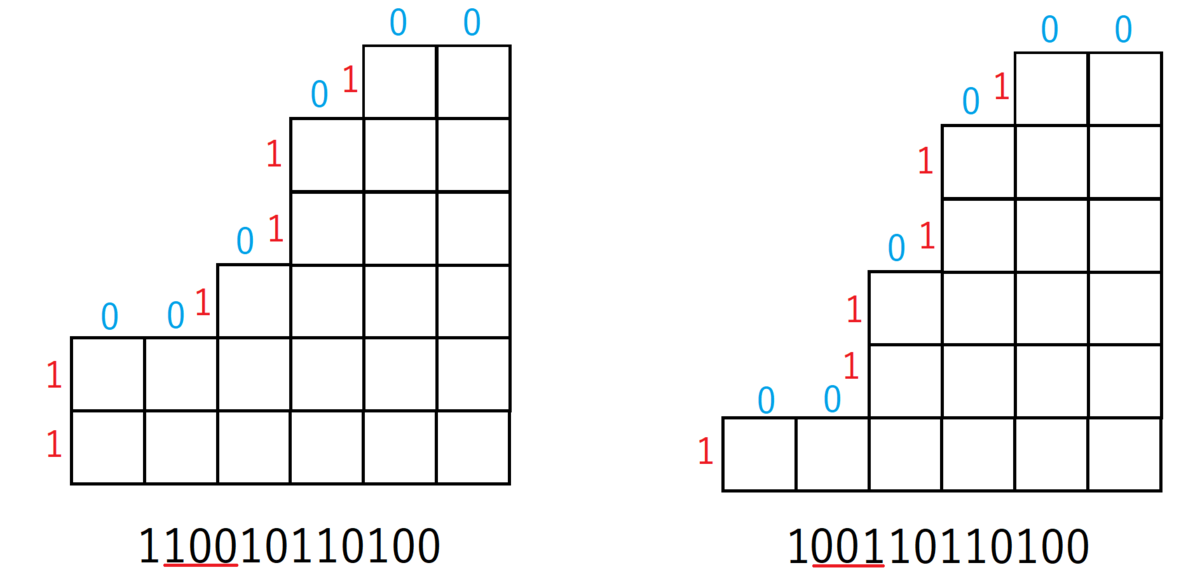
これらの操作を繰り返して、ソート完了済みの状態「000000111111」にするのに何通りの操作があるかが本問題の答えとなります。

「110」→「011」、「100」→「001」の操作はそれぞれ1つ飛ばしの「10」列を選んで「01」に変化させる操作になります。したがって、01列の偶数要素と奇数要素で分類させると、隣接する要素についてのみ考えることができ、見通しがよくなります。

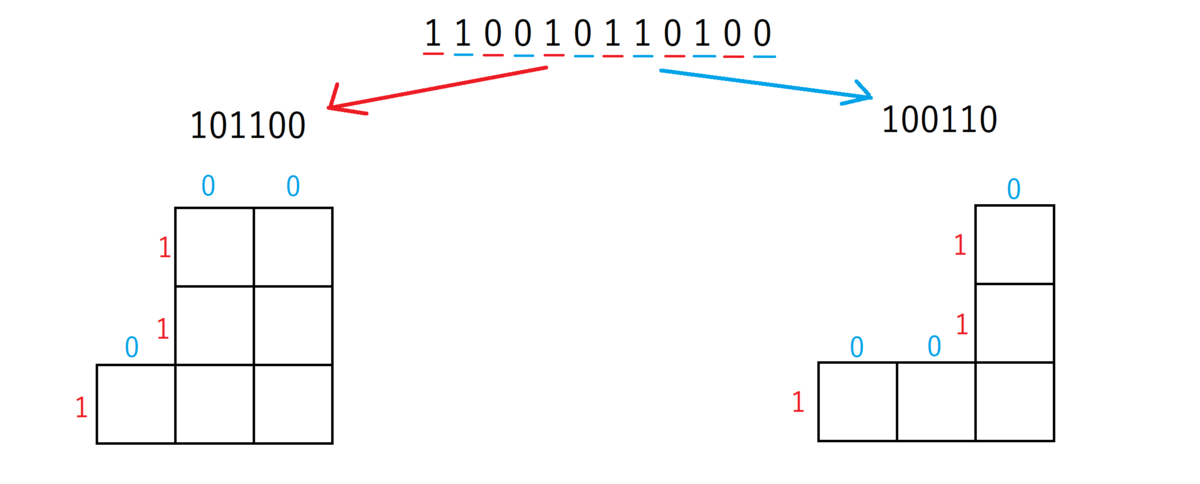
ここで、偶奇分類後の01列について、それぞれの「0」の前にある「1」の個数を箱に対応させた図を書くと、上図のようになります。隣接する「10」を選んで「01」にして、ソート完了済みの状態まで操作を行うことから、箱の合計は転倒数に一致します(0の前の1の個数の和をとっているのでそれはそう...)。
奇数列と偶数列の01文字列の転倒数の合計が全体で行う操作回数の合計になりますので、奇数列の転倒数を$M_1$、偶数列の転倒数を$M_2$とすると、$M_1 + M_2$の操作回数のうち奇数列と偶数列のどちらで操作を行うかを選ぶことになりますので、本問題の答えは、 $$ \binom{M_1 + M_2}{M_1} \times (奇数列をソート完了済みにする操作方法の数)\times (偶数列をソート完了済みにする操作方法の数) $$ となります。

したがって、本問題は

01列が与えられます。隣接する要素を入れ換える操作を最小回数行って、ソート完了済みにするのに何通りの操作がありますか？

といった問題へと言い換えられました。最小回数である必要があるのは、「10」を「01」に変換する転倒数を1減らす操作しか許されておらず、「00」、「01」、「11」を入れ換えることは禁じられた操作を行っていることになるためです。

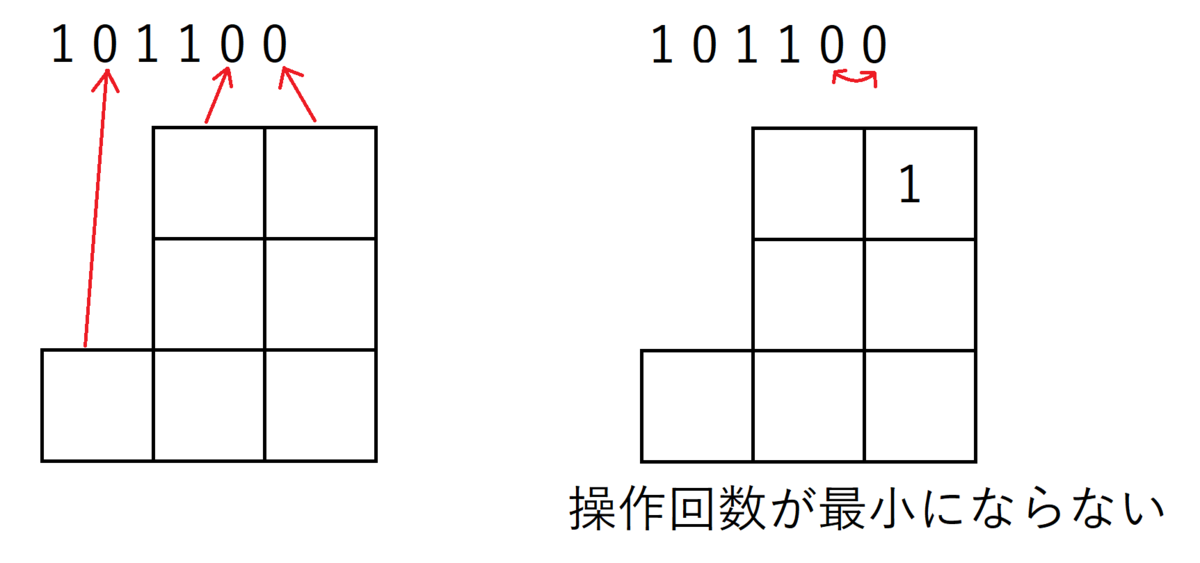
左から$i$番目に積みあがった箱の数に着目すると、これは「左から$i$番目の$0$の前にある$1$の個数」に相当します。すなわち、それぞれの$0$について何回操作を行えるかを表したものになります。
これらの箱に

同じ行にあるものでは左にあるものほど小さい
同じ列にあるものでは上にあるものほど小さい

といった制約のもので、何回目にその$0$についての操作を行うかの番号を書いていき、全体を埋める場合の数が操作方法の場合の数に一致します。（仮にもし、同じ行について左にあるものよりも先に小さい数を書いてしまったら、「00」のswapによって、0の追い越しが発生してしまい操作回数は最小とはならないことになります。）

話を戻すと、この左上ほど小さい数が来るように数を書き込んだ最終的な状態の数を効率よく求めることができるのがフック長の公式です。(原義のヤング図形では単調減少数列を上から並べたものに対して左上ほど小さい数を書き込むことになりますが、今回は後ろから操作を決め打っていると考えると同じものを数えていることになります。)
フック長の公式は、次元(最終的な状態数)を$d_{\lambda}$、全体の箱の数を$n$、$i$行目、$j$列目のフック長を${\rm hook}(i, j)$とすると、以下の式で表されます。

$$ d_{\lambda} = \frac{n!}{\prod {\rm hook}(i, j)} $$

箱の数$n$の階乗をフック長の総積で割ったものになります。
フック長とは、この図で言うと左にある箱の数、上にある箱の数に自分自身を加えたものになります。「101100」で表される箱について、左から2番目、下から1番目にある箱では左に1つ、上に2つ、自分自身1つでフック長は$4$となります。

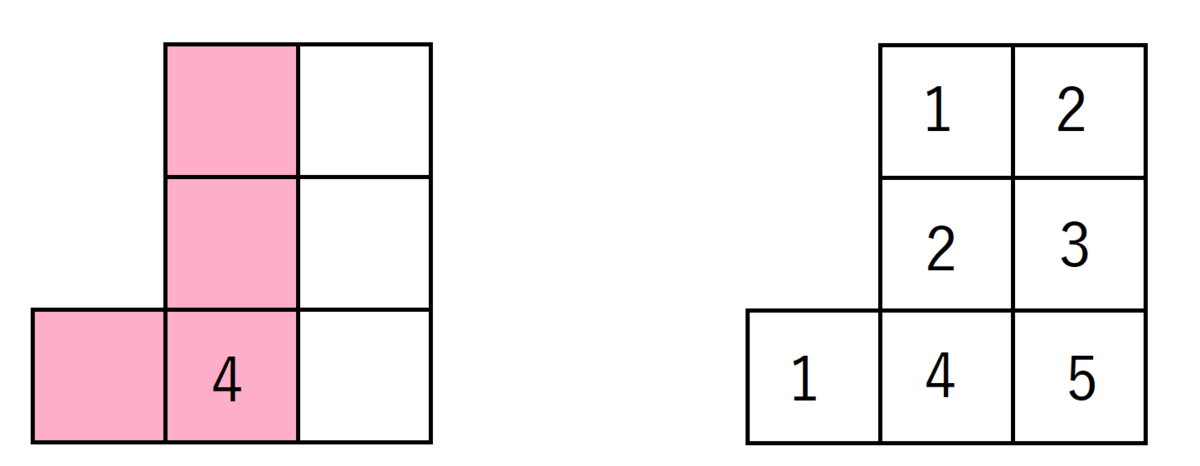
これをすべての箱に対して行い、フック長の公式に代入すると、

$$ d_{\lambda} = \frac{7!}{1\times 1\times 2\times 4\times 2\times 3\times 5} = 21 $$

となり、操作番号を書き込む、最終的な状態の数は21と求められました。すなわち、奇数列の「101100」に対して最小回数の隣接swapを行いソート完了済みの状態にするには21通りの方法があると言えます。

同様に、偶数列の「100110」に対して操作方法の数をフック長の公式から求めると、

$$ d_{\lambda} = \frac{5!}{1\times 2 \times 1 \times 2 \times 5} = 6 $$ で6通りの方法があります。

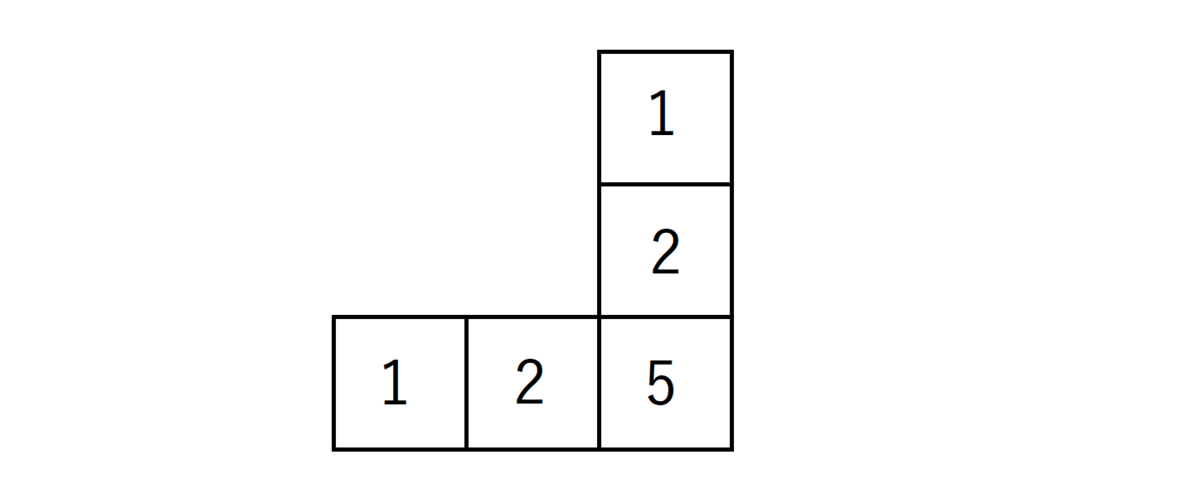
したがって、奇数列の箱の数は7個、偶数列の箱の数は5個でしたので、

6
2 2 3 5 6 6

に対する操作の数は、

$$ \binom{7 + 5}{7}\times 21 \times 6 = 792 \times 21 \times 6 = 99792 $$ 通りとなります。

余談になりますが、AtCoderの「Judge System Update Test Contest 202004」のC問題でヤング図形に対する数の書き込み方の個数を求める問題が出題されていたようです。(私が初見で解いたときは、順列全探索で間に合う制約だったので特に意識しませんでした。)

atcoder.jp

同じWriterさんが2ヶ月ほど前にyukicoderに出題なさっていた「No.2092 Conjugation」なんかもフック長の計算に役立ちそうです。

yukicoder.me

(私は本問題のフック長の計算の際に、上に積まれている箱の数ではなく下に積まれている箱の数を数えてしまいサンプルは合ったのに通らないといった事態が発生しました。もし同じ事態に直面している方がいらっしゃったらこれらの類題で確認してみると良いかもしれないです。)

続いて、0通りとなる場合、すなわち、操作を行ってもすべての要素を$0$とできない場合について考えます。これは、結論から言うと、奇数列、偶数列に対してそれぞれ操作を1回行う度に数列の合計が2減ることになりますので、 $ 2\times(M_1 + M_2) \neq \sum A_i $ のときに、0通りとなります。

私はこのことについて、すべての数列の要素の和が奇数の場合、0通りになるかと考えました。もとの01列を考えると「110」→「011」、「100」→「001」となり、全体の転倒数が2減ることになります。したがって、もとの01列における0の前にある1の個数は$A_i$に一致しますので、$\sum A_i \bmod 2 \neq 1$ が条件ではないかと考えました。
しかし、「1 2 3 4」→「10101010」のように、$A_i$ の要素の合計が偶数であり、奇数列と偶数列それぞれソート済みであるのにも関わらず、0と1の数に偏りがあるため「00001111」の最終状態までもっていくことができないものがあります。したがって、全体で操作できる回数から考える必要がありました。

実装例

実装には、AtCoder Libraryのmodint998244353を用いています。
また、二項係数の分母とフック長の公式の分子で両者の階乗が打ち消されるため、二項係数のための階乗の前計算等は行っていません。

#include <atcoder/all>
using namespace std;
using mint = atcoder::modint998244353;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    vector<int> A(n + 1);

    //01文字列の生成
    string str;
    for(int i = 1; i <= n; i++){
        cin >> A[i];
        str += string(A[i] - A[i - 1], '1') + "0";
    }

    //奇数要素と偶数要素についてそれぞれヤング図形を生成
    //s0, s1にはヤング図形の箱の合計(転倒数)が保持されている
    int cnt = 0, s0 = 0, s1 = 0;
    vector<int> odd, even;
    for(int i = 0; i < str.size(); i += 2){
        if(str[i] == '0'){
            odd.push_back(cnt);
            s0 += cnt;
        }else cnt++;
    }
    cnt = 0;
    for(int i = 1; i < str.size(); i += 2){
        if(str[i] == '0'){
            even.push_back(cnt);
            s1 += cnt;
        }else cnt++;
    }

    //条件の確認
    if(2 * (s0 + s1) != accumulate(A.begin(), A.end(), 0)){
        cout << 0 << '\n';
        return 0;
    }

    //フック長の積を計算(odd_v, even_v)に格納
    mint odd_v = 1, even_v = 1;
    vector<int> odd_cnt(1001), even_cnt(1001);
    for(int i = 0; i < odd.size(); i++){
        for(int j = 0; j < odd[i]; j++){
            odd_v *= odd[i] - j + odd_cnt[j];
            odd_cnt[j]++;
        }
    }
    for(int i = 0; i < even.size(); i++){
        for(int j = 0; j < even[i]; j++){
            even_v *= even[i] - j + even_cnt[j];
            even_cnt[j]++;
        }
    }

    mint ans = 1 / (odd_v * even_v);
    for(int i = 1; i <= s0 + s1; i++)ans *= i;

    cout << ans.val() << '\n';
}